Induced Yaw

Yaw is a funny thing.  As stated later in this article, An airplane is not always going in the same direction that it is pointing, and, in aircraft (unlike cars, bikes, or sailboats) you have separate control over which way it is pointing relative to which way it is going .  Following is a discussion of the Yaw phenomenon found on the World Wide Web.  Enjoy.

Overview

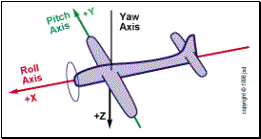
This article discusses the motion of the airplane around the yaw axis.   The conventional definitions of the three principal axes are shown below

Safety: Whereas if you stall in coordinated flight the nose will just drop straight ahead, if you manage to stall in sufficiently uncoordinated flight, you will get a spin  or a snap roll, which is much harder to recover from.  So pilots speak of "zero slip/skid angle'' and "good coordination'' almost interchangeably.

This section considers, one by one, the various phenomena  that affect the airplane's motion around the yaw axis.  There are surprisingly many such phenomena, including:

The corkscrewing slipstream

Yaw-axis inertia

Adverse yaw

P-factor

Gyroscopic precession

Stability and damping created by the vertical fin and rudder

Yaw Stability

An airplane is not always pointing in the same direction as it is going.  This is a new concept for most people, since for ordinary objects such as cars, bicycles and sailboats, the direction they are pointing is (more or less) always the same as the direction they are going, and certainly there is no separate control of

the two directions.

As an extreme example of the new concept, take a Frisbee and draw on it the picture of an airplane.  When you throw the Frisbee, the picture of the airplane will turn around and around and around.  The direction it is pointing has no connection with the direction it is going.

In a sailboat or airplane, you can change the heading with the rudder.  In the airplane (unlike the sailboat) the resulting sideways forces are too small to be of much use in changing the direction of motion.

Figure 2 shows a situation where the airplane's heading has been disturbed out of its usual alignment with the airflow.  There are lots of ways this could happen, including a gust of wind, a momentary uncoordinated deflection of the controls, or whatever.  In this situation, the relative wind is striking the vertical fin and rudder at an angle.  Like any other airfoil, the fin/rudder produces lift in proportion to its angle of attack, so it will produce a force (and therefore a torque) that tends to re-align the airplane with the wind.  We say that the airplane has lots of yaw-axis stability.  The colloquial name for yaw-axis stability is weather-vaning

 Weather-vaning: definition

The airplane tends to align itself with the relative wind, just as a weathervane does.

Yaw Damping

Pure yawing motions are reasonably well damped.  The process is analogous to the process that produces damping of pure vertical motions and pure rolling motions.   When the tail is moving to the right with an appreciable velocity, it sees a relative wind coming not from straight ahead, but from ahead and to the right.  The resulting angle of attack produces a leftward force.  A leftward force in proportion to a rightward velocity is exactly what constitutes damping.

Corkscrewing Slipstream

One of the very first things that people find out about when they start learning to fly is that it takes right  rudder (sometimes a lot of right rudder) to keep the airplane going straight at the beginning of the takeoff roll.  The physics of the situation is shown below.

You don't notice the effect of the corkscrewing slipstream in cruise, because the aircraft designers have anticipated the situation.  The vertical fin and rudder have been installed at a slight angle, so they are aligned with the actual airflow, not with the axis of the aircraft.

In a high-airspeed, low-power situation (such as a power-off descent) the built-in compensation is more than you need, so you need to apply explicit left rudder (or dial in left-rudder trim) to undo the compensation and get the rudder lined up with the actual airflow.

Conversely, in a high-power, low-airspeed situation (such as initial takeoff roll, or slow flight) the corkscrew is extra-tightly wound, so you have to apply explicit right rudder.

P-Factor

The situation is depicted in the figure above.  The airplane is in level flight, with a 10 degree nose-up attitude.  The motion of the blade through the air is the resultant found by adding the rotational motion (perpendicular to the thrust line of the aircraft) and the motion of the airplane as a whole (horizontal).  The motion of the downgoing blade is shown with solid lines, while the motion of the upgoing blade is shown with dotted lines.  You can see that the downgoing resultant is longer than the upgoing resultant.

This is the real story on P-factor: the advancing blade sees more relative wind, while the retreating blade sees less relative wind.

P-Factor Myth #1

There are quite a lot of myth surrounding P-factor.  For some reason, P-factor gets blamed for the fact that aircraft require right rudder on initial takeoff roll.  This is impossible for several reasons. 

Nearly everybody these days learns to fly in nose-wheel type aircraft (tricycle gear arrangement) so the propeller disk is vertical throughout the takeoff roll.  P-factor obviously cannot occur.

Now let's suppose, just for sake of argument, that you are flying a taildragger, in which the propeller disk is actually non-vertical during the initial takeoff roll.  Common experience is that the most right rudder is required at the very beginning of the takeoff, before much forward speed has been achieved.  The Flight Training Handbook says this is because P-factor is worst at low airspeeds. But wait a minute --- real P-factor is proportional to airspeed.  In the initial moments of the takeoff roll, there is no relative wind, so there can't possibly be any P-factor.  Of course, if you are taking off into a headwind, there could be a little bit of P-factor --- but does that mean if you take off with a slight tailwind there will be a negative amount of P-factor, requiring left rudder?  Don't bet on it.

The real reason that you need right rudder on initial takeoff roll is because of the corkscrewing slipstream.   P-factor exists in principle, but it cannot possibly explain the behavior we observe in real airplanes.

P-Factor Myth #2

Nearly all pilots have been taught that P-factor has something to do with the angle of attack of the right (downgoing) and left (upgoing) propeller blades.  I'm sorry to slaughter so many sacred cows, but this one has got to go.  The situation is analyzed in below.

Many uncareful references point out that the downgoing blade makes a bigger angle to the vertical than does the upgoing blade.  Alas, that doesn't explain anything. The blade doesn't care which way is up --- all it cares about is where the relative wind is coming from.   You can incline the propeller disk as much as you want relative to vertical, but there will be no P-factor in the absence of relative wind.

P-Factor Myth #3

P-factor also gets blamed for "critical engine'' effects in multiengine aircraft.  I have two things to say about this:

Yes, P-factor really does occur.

Sorry, it is negligible compared to the corkscrewing slipstream effect.

I estimated the amount of P-factor for a Piper Apache:

The corkscrewing slipstream may not seem like a big effect either, but remember that it operates by striking the rudder, which is large and has tremendous leverage. 

Since both P-factor and corkscrewing slipstream can both occur, I suggest the following experiment to see which is more significant. Take your favorite aerobatic airplane and paint the starboard rudder pedal green and the port rudder pedal red, just so we can keep straight which is which.  Now go to a safe altitude and set up for “inverted” slow flight.  In this high-power, low-speed situation, you need to push the port (red) pedal or the starboard (green) pedal?  If you believe in P-factor, the answer will be port, because that is now the downgoing, advancing blade. If you believe that the corkscrewing slipstream is more important, the answer is starboard, because the relationship between the propeller, rudder, and rudder pedals is unchanged by the inversion.

Gyroscopic Precession

A spinning object will respond to a torque around one axis with a motion around another axis.  This remarkable and counterintuitive phenomenon.

Gyroscopic precession is often quite noticeable at the point where a taildragger raises the tail, early in the takeoff roll. 

If the airplane were an ordinary non-spinning object, you could raise the tail using the elevators alone.  The elevators do not actually dictate the “motion”  of anything; they just produce a “force” and a torque around the pitch axis.  For a gyroscope, a torque around the pitch axis produces a motion around the yaw axis.  If you try to raise the tail of a real airplane using elevators alone, it will yaw to the left because of precession.  To get a gyroscope to actually “move”  around the pitch axis, you need to apply a force around the yaw axis --- using the rudder.

Of course, an airplane has some plain old mass in addition to its gyroscopic properties.  In order to lift this ordinary mass you need to use the elevators.  Therefore, the tail-raising maneuver requires both elevators and rudder --- elevators to change the pitch of the ordinary mass, and rudder to change the pitch of the gyroscope.

Rudder Usage During Rolls

Every pilot knows that turning the airplane properly requires coordinated use of ailerons and rudder. Getting it exactly right is a bit tricky.

Remember that in an airplane, the direction you are moving is not necessarily the same as the direction you are pointing.

There are several crucial things that happen during a turn:

1)       You use the wings to change the direction of motion of your center of mass.  I call this the “CM-turn”

2)       You use the rudder to change your heading (i.e. to overcome yaw-axis inertia, i.e.  to provide yaw-axis acceleration)

3)       You use the rudder to overcome adverse yaw.

Item 1 is relatively straightforward: you put the airplane into a bank.  The horizontal component of lift will change the direction of motion.

If lift were the only force involved, banking the airplane would cause it to just “slip” off in the new direction without changing its heading.  Therefore you apply the rudder to cause an angular acceleration around the yaw axis, creating a yaw rate that matches the CM-turn rate.

Finally, we must consider adverse yaw, which is a relatively minor contribution, it can only exist during the fraction of a second after the ailerons have been deflected and “before”  the airplane has established a steady roll rate.  After a “steady” roll rate is established, then the lift of the two wings must be the same.  (Remember, an unbalanced torque would cause an “acceleration” around the roll axis, not a steady roll.) If the lift is the same, the drag must be the same, so during a “steady” roll, adverse yaw is negligible compared to yaw-axis inertia.

For any given rate of roll, the required yaw-axis acceleration is greater at low airspeeds.  This is because for any given bank, the rate of turn is greater at low airspeeds.  A similar statement applies to adverse yaw adverse yaw is more pronounced at low airspeeds.  These facts can be combined in one rule: you need to use lots of rudder at low airspeeds.

Analysis of a Roll

To make the discussion more concrete, let's consider a roll starting from straight-and-level flight and rolling to the right.  As we can see from the figure below

Of course, if you move the ailerons really, really slowly, then the yaw axis will pretty much take care of itself.  Of course I recommend flying with a smooth,  gentle touch --- but it is worth examining what happens if you move the ailerons fairly abruptly:

(1)     there will be times when you want to roll the airplane on short notice, so let's learn how to do it;

(2)     the abrupt case makes it easier to understand what is going on.

In some airplanes, such as a Piper Cub, the roll rate will reach its final very quickly (within half a second or so), because the airplane has very little inertia about the roll axis.  All the mass (pilot, passenger, fuel, and engine) is arranged in a straight line right on top of the roll axis, so they don't contribute much moment of inertia. In other airplanes, such as a Cessna 310, the roll rate responds much more slowly, because lots of mass (engines and tip tanks) is situated far from the roll axis.

Before the roll rate is established (i.e. during the time [t1, t2]) the plane will experience more or less pure adverse yaw.  The nose will swing a little toward the outside of the turn.  The effect is usually rather small, since (a) induced-drag forces are typically a hundred times smaller than lift forces, and (b) these forces must act against the yaw-axis inertia, which is at least as large as the roll-axis inertia.

In a Piper Cub, the yaw-axis inertia is quite large compared to the roll-axis inertia.  Even in the Cessna 310, where the roll-axis inertia is large, the yaw-axis inertia is still larger.  (This is because almost anything that contributes to roll-axis inertia also contributes to yaw-axis inertia, for any reasonable shape of airframe).

The rest of the discussion applies whether or not you moved the ailerons abruptly.

After the time t2, a steady roll rate exists.  Even though the ailerons are deflected, there is no difference in lift from one wing to the other.  (The effect of the ailerons is canceled by the fact that the air is hitting the two wings at different angles.)  Since there is no difference in lift, there will be no difference in induced drag, hence no adverse yaw.

However, because the airplane has been rolling for a while, a bank has developed.  This bank creates a horizontal component of lift, which in turn deflects the direction of flight --- i.e. causes a CM-turn.

We assume that (for the sake of the experiment) you have not used the rudder during this maneuver so far.  So, even though the airplane is moving in a new direction, the heading hasn't changed (or has even changed slightly in the wrong direction, due to adverse yaw).  The airplane has a nonzero slip/skid angle.  The uncoordinated airflow acting on the rudder will now, only now, begin to get the airplane pointed in the right direction.  The airflow will remain uncoordinated until the roll stops.  If the yaw axis damping is weak, as it usually is, the nose will slosh back and forth through the "right'' heading several times.

To make a coordinated turn, you have to use the rudder.

From time t2 through t5, there is a steady roll rate.  Since the angle of bank is increasing, the CM-turn rate is increasing proportionately.  To match this, you need a steadily-increasing yaw rate.  The airplane is just like a toy top; if you want to make it spin faster you have to supply a torque.  Steady right rudder pressure is the proper way to provide the torque needed to create this steadily-increasing yaw rate.

At time t6, the ailerons are neutralized, but the rolling motion has not yet stopped.  (Again, there is a delay due to roll-axis inertia.) There is a difference in lift between the two wings, as needed to damp out the roll.  This creates a negative amount of adverse yaw.  You might think left rudder is required to cancel this adverse yaw (assuming the ailerons were neutralized suddenly) --- but you might also think that right rudder is required (because the airplane is still rolling, and a still-increasing rate of yaw is needed to coordinate with the still-increasing rate of CM-turn).  In fact the latter phenomenon dominates in practical situations.

Analogous statements would apply if you started from a left turn and used right aileron and right rudder to roll out of the turn. Similarly, it is easy to do a similar analysis for rolling into a left turn and/or rolling out of a right turn.

Designers Tricks

Imagine an airplane without a vertical fin.  It would behave be more like a Frisbee than a sailboat --- if you gave it a yaw rate, inertia would make it just keep on yawing until some torque acted to stop it.  By the same token, if it started with zero yaw rate, inertia would keep it from yawing unless some definite torque were applied.

In a real airplane, of course, the vertical fin and rudder supply the forces required to keep the yaw angle and yaw rate under control.

Aircraft manufacturers know about yaw-axis inertia and its effects on turns.  They generally try to provide the needed yaw-axis acceleration automatically, using various tricks.  One trick is to interconnect the rudder and ailerons with a spring.  That means you automatically get a certain amount of rudder deflection in proportion to the aileron deflection.  They choose the proportionality factor so that you can more or less fly "with your feet on the floor'' at cruise airspeeds. Of course, vastly more rudder is needed at lower airspeeds; fortunately you can easily overpower the interconnect spring by pushing on the controls in the obvious way.

Here's another trick, which you may have noticed on many airplanes: when one aileron goes down a little, the other one goes up a lot. (This is called “differential aileron deflection” .)  The designers were trying to arrange for the upward-deflected aileron to generate a lot of parasite drag.  If they do it just right,  the drag force is just enough to provide the needed yaw-axis acceleration during a steady roll.  The so-called “Frise aileron” is similar, but it has lip that sticks down into the airstream when the main part of the aileron is deflected up.  Again, the purpose of the lip is to generate drag on the wing with the upward-deflected aileron.

In addition to overcoming yaw-axis inertia (during a steady roll), the designers also want to overcome adverse yaw (when ailerons have been deflected but the roll hasn't yet started).  Fortunately, genuine adverse yaw is very small, and by adjusting the amount of differential deflection, and the amount of the Frise effect, pretty good cancellation can be achieved.

The bad news is that this compensation only works at one airspeed. The designers arrange it so you can fly with your feet on the floor during cruise.  This is a mixed blessing, because it can lull you into complacency.  At lower airspeeds, where it is most important, you still need to use lots of rudder to keep things coordinated.   Don't forget!

The Origins of Adverse Yaw

Suppose you wish to roll into a right turn.  You will deflect the ailerons to the right, as shown below

Once the airplane is established in a steady turn, or even in a steady roll rate (no acceleration around the roll axis), the two wings are producing the same amount of lift, so there will be no adverse yaw.

Now let's consider what happens if you wish to roll out of the turn. The airplane is banked to the right and already turning to the right. You will deflect the ailerons to the left.  This will cause extra drag on the right wing, and reduced drag on the left wing. The airplane will yaw to the right, continuing and exaggerating the turn that you were trying to stop.  Anticipating this, you apply left rudder along with the left aileron.

Amount of Adverse Yaw

The amount of adverse yaw you expect is proportional to the amount of aileron deflection, but also depends on your airspeed, or more precisely on your angle of attack.  The key to understanding this is to realize that whereas the coefficient of lift is more or less proportional to the angle of attack (for moderate angles of attack), the coefficient of induced drag is more or less proportional to the square of the angle of attack.

The left side of the figure shows the same situation as in the previous figure, along with the coefficient of drag curve. On this curve I have indicated the different angles of attack for the two wingtips, and the correspondingly different amounts of drag.  We see that the coefficient of drag curve is relatively flat on the bottom, so at relatively small angles of attack (high airspeeds), a difference in angle of attack doesn't cause too much difference in drag.

In contrast, the right side of the figure shows the same aircraft in slow flight.  Both wings are operating at a higher angle of attack.  Because the coefficient of drag curve is steeper in this regime, the same difference in angle of attack (i.e. the same aileron deflection) creates more difference in drag (i.e. more adverse yaw).

Summary:  Coordinated Turning Procedures

A proper turn consist of two ingredients: a CM-turn and a heading change.  In an idealized "basic'' airplane, you would use the ailerons to bank the airplane and lift the CM around the turn, and use the rudder to change the heading.  In a typical modern airplane at cruise airspeeds, deflecting the ailerons alone creates a fair approximation of the proper torques around both axes.  In all airplanes at low airspeeds, proper rudder sage is vitally important.

The basic rule is simple:   if you are rolling to the right, you must apply right rudder; if you are rolling to the left, you must apply left rudder.  The amount of rudder will depend inversely on the airspeed.

From and article published on the World Wide Web